Part 1: Linked Lists
Learning Objectives
-
Students Will Be Able To:
- Define linked lists
- Explain the time complexity of linked list operations
- Compare and contrast linked lists to Arrays
- Visualize a linked list
- Traverse a singly linked list
- Remove nodes from a singly linked list
Roadmap
- Setup
- Defining a linked list
- Linked list operation time complexity
- Comparing linked lists to arrays
- Review JS class syntax
- Linked list visualization
- Meet the walker
-
Use the walker to remove nodes
Defining a Linked List

Linked lists are a foundational, "array-like" data structure which appears in other complex data structures
-
Linked lists are a collection of nodes
- nodes are also seen in other data structures, but for linked lists, they contain:
- a
dataproperty, that stores the node's value - a
nextproperty, also known as the "pointer", which points to the next item in the linked list - the last node will have a
nextproperty set tonull, so it is sometimes referred to as the "null next node", or the "tail"
Because of the pointers, the order of nodes within a linked list are not given by their physical placement in memory
Linked List Operation Time Complexity
| Operation | Worst Case Time Complexity |
|---|---|
| Indexing (Access) | O(N) |
| Insert/delete at beginning | O(1) |
| Insert/delete at end | O(1) when last element is known |
| Insert/delete in middle | search time + O(1) |
Comparing Linked Lists to Arrays
It seems that linked lists are very similar to arrays, but have natural drawbacks
- ❓ What is the time complexity of indexing for an array?
- ❓ Is it possible for us to look backwards through a linked list where each node only has a data and next property?
But for us to understand the advantages of linked lists, we'll have to do a bit of a review of arrays
For this lesson, we'll be discussing dynamic arrays, instead of static arrays
-
A dynamic array stores all elements consecutively in memory, and keeps a count of the current number of elements
- arrays are allocated space when defined
- if the space reserved for the dynamic array is exceeded, it is reallocated and (possibly) copied

- If we want to insert something into an array, we have to make space by "scooting over" every element, starting at the index we want to insert at
- ❓ What must we do if we want to delete an element in the middle of the array?
- ❓ What are some of the advantages of linked lists over arrays?
Visualizing a Linked List
-
When we create a linked list, we initialize it with a
headproperty, which will refer to the first node- When you initialize a linked list, head will not point to anything yet, so it will point to
null
- When you initialize a linked list, head will not point to anything yet, so it will point to
-
The easiest place to add more nodes to the linked list is at the end of the list
- ❓ How do we know if you have reached the end of a linked list?
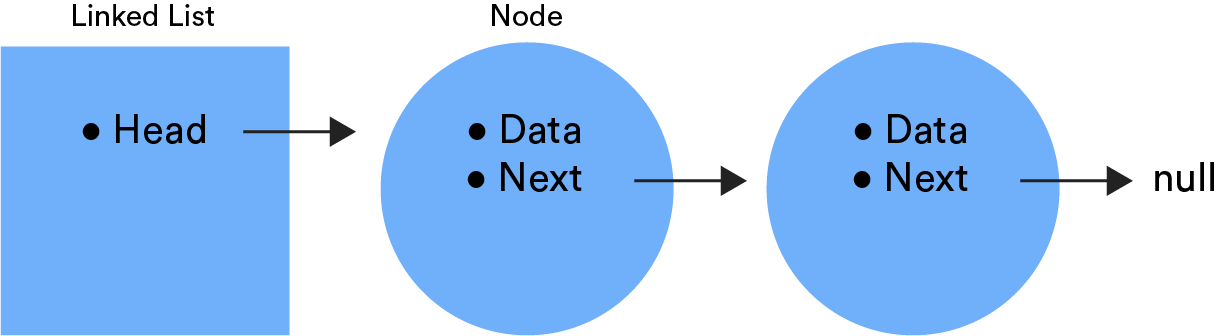
We will be referring to this graphic for the below sections
Node Class API
| Function | Arguments | Returns | Directions | Example |
| constructor | (Data, Node) | Node | Creates a class instance to represent a node. The node should have two properties, 'data' and 'next'. Accept both of these as arguments to the 'Node' constructor, then assign them to the instance as properties 'data' and 'next'. If 'next' is not provided to the constructor, then default its value to be 'null'. |
const n = new Node('Hi');
n.data // 'Hi'
n.next // null
const n2 = new Node('There', n);
n.next // returns n
|
LinkedList Class API
| Function | Arguments | Returns | Directions | Example |
| constructor | - | (LinkedList) | Create a class to represent a linked list. When created, a linked list should have *no* head node associated with it. The LinkedList instance will have one property, 'head', which is a reference to the first node of the linked list. By default 'head' should be 'null'. |
const list = new LinkedList();
list.head // null
|
| insertFirst | (data) | - | Creates a new Node from argument 'data' and assigns the resulting node to the 'head' property. Make sure to handle the case in which the linked list already has a node assigned to the 'head' property. |
const list = new LinkedList();
list.insertFirst('Hi There'); // List has one node
|
| size | - | (integer) | Returns the number of nodes in the linked list. |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.insertFirst('c');
list.size(); // returns 3
|
| getFirst | - | (Node) | Returns the first node of the linked list. |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.getFirst(); // returns Node instance with data 'a'
|
| getLast | - | (Node) | Returns the last node of the linked list |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.getLast(); // returns node with data 'a'
|
| clear | - | - | Empties the linked list of any nodes. |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.clear();
list.size(); // returns 0
|
| removeFirst | - | - | Removes only the first node of the linked list. The list's head should now be the second element. |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.removeFirst();
list.getFirst(); // returns node with data 'a'
|
| removeLast | - | - | Removes the last node of the chain |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.removeLast();
list.size(); // returns 1
list.getLast(); // returns node with data of 'b'
|
| insertLast | (Data) | - | Inserts a new node with provided data at the end of the chain |
const list = new LinkedList();
list.insertFirst('a');
list.insertFirst('b');
list.insertLast('c');
list.getLast(); // returns node with data 'C'
|
| getAt | (integer) | (Node) | Returns the node at the provided index |
const list = new List();
list.insertFirst('a');
list.insertFirst('b');
list.insertFirst('c');
list.getAt(1); // returns node with data 'b'
|
| removeAt | (integer) | - | Removes node at the provided index |
const list = new List();
list.insertFirst('a');
list.insertFirst('b');
list.insertFirst('c');
list.removeAt(1);
list.getAt(1); // returns node with data 'a'
|
| insertAt | (Data, integer) | - | Create an insert a new node at provided index. If index is out of bounds, add the node to the end of the list. |
const list = new List();
list.insertFirst('a');
list.insertFirst('b');
list.insertFirst('c');
list.insertAt('Hi', 1)
list.getAt(1); // returns node with data 'Hi'
|
// Linked list
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertFirst(data) {
this.head = new Node(data, this.head);
}
size() {
let counter = 0;
let node = this.head;
while (node) {
counter++;
node = node.next;
}
return counter;
}
getFirst() {
return this.head;
}
getLast() {
if (!this.head) {
return null;
}
let node = this.head;
while (node) {
if (!node.next) {
return node;
}
node = node.next;
}
}
clear() {
this.head = null;
}
removeFirst() {
if (!this.head) {
return;
}
this.head = this.head.next;
}
removeLast() {
if (!this.head) {
return;
}
if (!this.head.next) {
this.head = null;
return;
}
let previous = this.head;
let node = this.head.next;
while (node.next) {
previous = node;
node = node.next;
}
previous.next = null;
}
insertLast(data) {
const last = this.getLast();
if (last) {
// There are some existing nodes in our chain
last.next = new Node(data);
} else {
// The chain is empty!
this.head = new Node(data);
}
}
getAt(index) {
let counter = 0;
let node = this.head;
while (node) {
if (counter === index) {
return node;
}
counter++;
node = node.next;
}
return null;
}
removeAt(index) {
if (!this.head) {
return;
}
if (index === 0) {
this.head = this.head.next;
return;
}
const previous = this.getAt(index - 1);
if (!previous || !previous.next) {
return;
}
previous.next = previous.next.next;
}
insertAt(data, index) {
if (!this.head) {
this.head = new Node(data);
return;
}
if (index === 0) {
this.head = new Node(data, this.head);
return;
}
const previous = this.getAt(index - 1) || this.getLast();
const node = new Node(data, previous.next);
previous.next = node;
}
// If your hungry for more
forEach(fn) {
let node = this.head;
let counter = 0;
while (node) {
fn(node, counter);
node = node.next;
counter++;
}
}
// If your absolutely starving
*[Symbol.iterator]() {
let node = this.head;
while (node) {
yield node;
node = node.next;
}
}
}Part 2: Stacks & Queues
Overview
This lesson covers an introduction to the concept of Stacks and Queues.
Learning Objectives
By the end of this lesson, you will be able to:
- Distinguish between the behavior of a stack and a queue.
- Determine situations in which you’d use a stack or queue versus another data structure.
- Build a stack and a queue using a linked list or an array.
What are Stacks & Queues?
Stacks and queues in computer science are a lot like stacks and queues in real life. It helps if you think of stacks of pancakes and queues, or lines, of people.
Queues
Let’s take a look. It’s Saturday morning, and out of the kindness of your heart you decide to make pancakes for your family. You’re gathering all the ingredients when you check the fridge and discover you’re out of eggs! You rush to the grocery store, grab the eggs, and of course the line to check out — the queue — is five-people deep. You move to the back and wait your turn.
Waiting in line for the cash register mirrors how a queue works in computer science. They’re defined by first-in, first-out behavior. That is, the first thing that’s added to a queue will be the first thing removed; the first person in line will be the first person who gets to check out.
Queues operate on "first-in, first-out" (aka, FIFO) behavior. Items are removed in the order they were added, from first to last.

Computer processing unit (CPU) scheduling is based on a queue. Tasks are executed in the order in which they were called, while the execution of tasks further down in the queue is put on hold until resources are available, on a first in, first out basis.
Stacks
Now for stacks. You’ve made it home and the pancakes are coming together beautifully. As you cook, you flip the pancakes off the griddle and onto a plate. You finish up the last batch and bring the pancakes to the table to serve your family. Which pancakes are going to be taken first? The hot, fresh pancakes on the top of the stack? Or the pancake on the bottom that’s now cold and getting smushed? We know which one we’d take — the hot one on the top.
Watching your family take the fresh pancakes off the top of the plate is how a stack works. A stack is defined by last-in, first-out behavior — the opposite of how a queue works. The last thing added to the stack — the freshest pancake — is the first thing to be removed.
Stacks operate on “last-in, first-out” (aka, LIFO) behavior. The last, most recently added item, is the first to be removed.
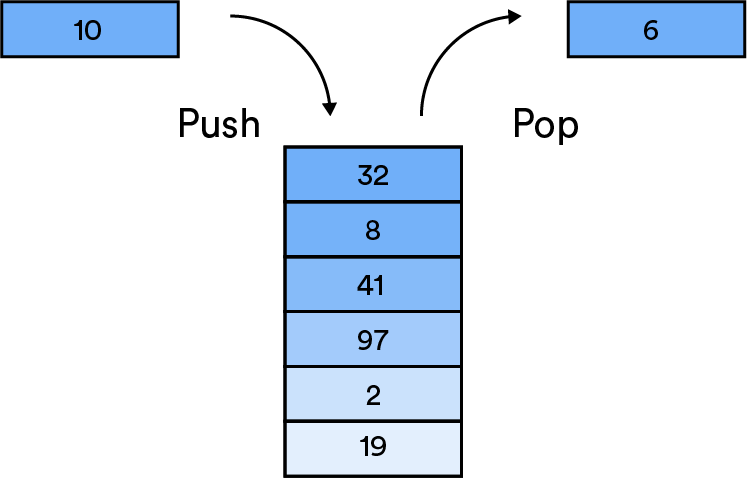
The function call stack is a common example of stacks in programming. When you call a function to execute, it’s pushed to the top of the stack and runs until we add another function to the stack, which then runs until it returns (or another function is pushed to the top), on a last in, first out basis. You can keep adding functions until you’ve run out of space in the stack, in which case you’ve reached stack overflow. (Mmm, pancake stack overflow... 😋)
❓ What data structure would be represented by the 'back' button in the browser?
❓ What data structure would be represented by sending documents to the printer?
❓ What data structure would be represented by the 'undo' or Cmd-Z function?
Operations in Stacks & Queues
Stacks and queues might seem totally different, but they actually have a lot in common.
One important similarity is that we can perform the same relatively limited set of actions on them.
The trade-off for limited functionality? Great runtimes, which are the same for stacks and queues! Check it out:
| Function | Name in a Stack | Name in a Queue | Complexity |
|---|---|---|---|
| Access | Peek | Peek | O(1) |
| Insert | Push | Enqueue | O(1) |
| Delete | Pop | Dequeue | O(1) |
| Check empty | isEmpty | isEmpty | O(1) |
❓ Imagine that you started with an empty stack and perform the following operations:
PUSH 0POPPUSH 2PUSH 4PUSH 6POPPUSH 8
...What would the stack look like at the end? (Hint: It might help to sketch this out on a piece of paper!)
❓ Imagine that you start with an empty queue and perform the following operations:
ENQUEUE 15DEQUEUEENQUEUE "Popcorn"ENQUEUE 515ENQUEUE "GA"DEQUEUEENQUEUE "Smile!"
...What would your queue end up looking like?
Implementing Stacks & Queues
The other thing that stacks and queues have in common is that they can both be implemented as an array or as a linked list.
Other than using different underlying data structures, there’s no major difference between array and linked list implementation. Which you use depends on how your data is already structured and how you expect to be inserting or removing elements.
For the implementations in this exercise, we'll be using array-based implementations.
❓ Quick refresher: The major difference between a linked list and an array is how they store data in a computer’s memory.
Which of the following statements is true about how linked lists and arrays store data? 🧐
- Linked lists store data in one continuous block of memory.
- Arrays store data in one continuous block of memory.
- Linked lists can store data anywhere in a computer's memory using pointers.
- Arrays can store data anywhere in a computer's memory using the index.
Queue Variations
Queues have a couple of unique implementations that we'll touch on.
Priority Queues
These have three rules in addition to regular queues:
- Every item has a priority associated with it.
- An element with high priority is dequeued before an element with low priority.
- If two elements have the same priority, they are served according to their order in the queue.
Examples: Airport priority boarding, CPU scheduling
Double-Ended Queues
A double-ended queue, or "deque", perform insertions and deletions at both ends of the queue. They're usually implemented with doubly-linked lists or dynamic arrays.
Have you ever been last in a long line at the grocery store only to see a cashier one lane over open up their register? Typically, that cashier will beckon to you to jump into their lane so you can be checked out right away. That’s basically what happens in a deque.
Example: spreading tasks between different servers as equally as possible
Essential Questions
❓ You're working on building a message board and want to display only the 10 most recent messages a user posted, in the order they were posted. Which data structure should you use?
❓ You and your partner are going out for your anniversary dinner. When you arrive, you ask the host for a table for two and your name goes on the waiting list. While you’re waiting, a group of seven people walks right in and gets seated. What gives?!
Interviews
If stacks or queues come up in an interview, you’ll likely be asked to perform operations such as sorting, inserting, and finding values — and it only gets more complicated from there.
- This article on stacks outlines some standard problems that could come up in interviews.
- The same article, but for queues.
- Don’t forget to review priority queues and deques. (You might not be asked to build one of these, mostly to explain how they work and their uses.)
Use these visualization tools to practice building stacks and queues:
- Stacks: array implementation and linked list implementation.
- Queues: array implementation and linked list implementation.
Array Implementation
stack
// --- Directions
// Create a stack data structure. The stack
// should be a class with methods 'push', 'pop', and
// 'peek'. Adding an element to the stack should
// store it until it is removed.
// --- Examples
// const s = new Stack();
// s.push(1);
// s.push(2);
// s.pop(); // returns 2
// s.pop(); // returns 1
class Stack {
constructor() {
this.data = [];
}
push(record) {
this.data.push(record);
}
pop() {
return this.data.pop();
}
peek() {
return this.data[this.data.length - 1];
}
}
module.exports = Stack;Queue
// --- Description
// Create a queue data structure. The queue
// should be a class with methods 'enqueue' and 'dequeue'.
// Adding to the queue should store an element until
// it is removed
// --- Examples
// const q = new Queue();
// q.enqueue(1);
// q.dequeue(); // returns 1;
class Queue {
constructor() {
this.data = [];
}
enqueue(record) {
this.data.unshift(record);
}
dequeue() {
return this.data.pop();
}
}
module.exports = Queue;Binary Search Trees



Simple BST implementation (Quick and dirty)
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
insert(data) {
if (data < this.data && this.left) {
this.left.insert(data);
} else if (data < this.data) {
this.left = new Node(data);
} else if (data > this.data && this.right) {
this.right.insert(data);
} else if (data > this.data) {
this.right = new Node(data);
}
}
contains(data) {
if (this.data === data) {
return this;
}
if (this.data < data && this.right) {
return this.right.contains(data);
} else if (this.data > data && this.left) {
return this.left.contains(data);
}
return null;
}
}Binary Search Tree properly implemented
Binary Search Tree (BST)
BST
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);Breadth First Search
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
bfs(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);
tree.bfs();Depth First Search
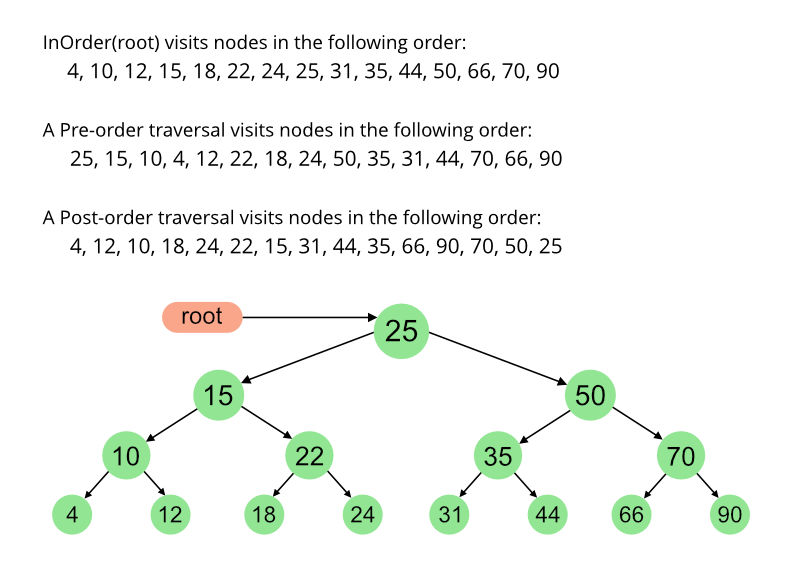
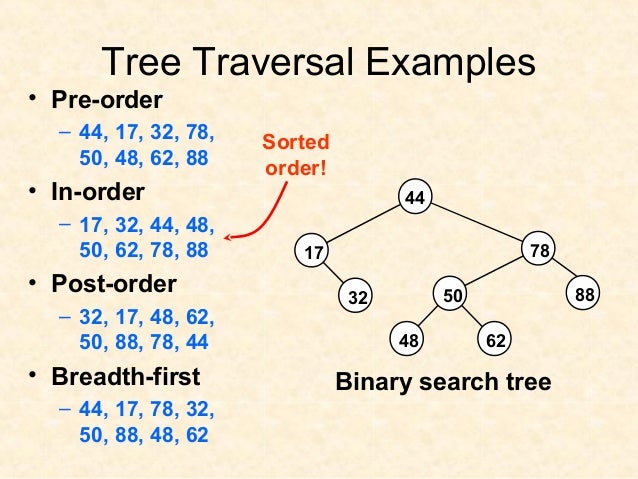
Algorithm Inorder(tree)
Traverse the left subtree, i.e., call Inorder(left->subtree) Visit the root. Traverse the right subtree, i.e., call Inorder(right->subtree)
Algorithm Preorder(tree)
Visit the root. Traverse the left subtree, i.e., call Preorder(left->subtree) Traverse the right subtree, i.e., call Preorder(right->subtree)
Algorithm Postorder(tree)
Traverse the left subtree, i.e., call Postorder(left->subtree) Traverse the right subtree, i.e., call Postorder(right->subtree) Visit the root
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(){
this.root = null;
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}
let current = this.root;
while(true){
if(value === current.value) return undefined;
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.left;
} else {
if(current.right === null){
current.right = newNode;
return this;
}
current = current.right;
}
}
}
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
found = true;
}
}
if(!found) return undefined;
return current;
}
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(current && !found){
if(value < current.value){
current = current.left;
} else if(value > current.value){
current = current.right;
} else {
return true;
}
}
return false;
}
bfs(){
let node = this.root,
data = [],
queue = [];
queue.push(node);
while(queue.length){
node = queue.shift();
data.push(node.value);
if(node.left) queue.push(node.left);
if(node.right) queue.push(node.right);
}
return data;
}
dfsPreOrder(){
let data = [];
function traverse(node){
data.push(node.value);
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
dfsPostOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
if(node.right) traverse(node.right);
data.push(node.value);
}
traverse(this.root);
return data;
}
dfsInOrder(){
let data = [];
function traverse(node){
if(node.left) traverse(node.left);
data.push(node.value);
if(node.right) traverse(node.right);
}
traverse(this.root);
return data;
}
}
const tree = new BinarySearchTree();
tree.insert(10);
tree.insert(6);
tree.insert(15);
tree.insert(3);
tree.insert(8);
tree.insert(20);
tree.dfsPreOrder();
tree.dfsPostOrder();
tree.dfsInOrder();Python Example
class TreeNode:
def __init__(self, value):
self.left = None
self.right = None
self.value = valueclass BST:
def __init__(self):
self.root = None
def get_root(self):
return self.root# ... inside of BST
def insert(self, value):
if self.root is None:
self.root = TreeNode(value)
else:
self._insert(value, self.root)
def _insert(self, value, node):
if value < node.value:
if node.left is not None:
self._insert(value, node.left)
else:
node.left = TreeNode(value)
else:
if node.right is not None:
self._insert(value, node.right)
else:
node.right = TreeNode(value) # ... inside BST
def find(self, value):
if self.root is not None:
return self._find(value, self.root)
else:
return None
def _find(self, value, node):
if value == node.value:
return node
elif (value < node.value and node.left is not None):
return self._find(_value_, node.left)
elif (value > node.value and node.right is not None):
return self._find(value, node.right) # ... inside BST
def delete_tree(self):
# garbage collector will do this for us.
self.root = None
def print_tree(self):
if self.root is not None:
self._print_tree(self.root)
def _print_tree(self, node):
if node is not None:
self._print_tree(node.left)
print(str(node.value) + ' ')
self._print_tree(node.right)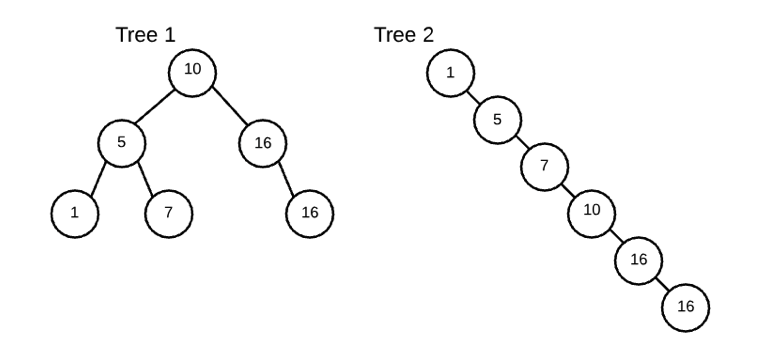
# Example 1
tree1 = BST()
tree1.insert(10)
tree1.insert(5)
tree1.insert(16)
tree1.insert(1)
tree1.insert(7)
tree1.insert(16)
tree1.print_tree()
print(tree1.find(3).value)
print(tree1.find(10))
tree1.delete_tree()
tree1.print_tree()
# Example 2
tree2 = BST()
tree2.insert(1)
tree2.insert(5)
tree2.insert(7)
tree2.insert(10)
tree2.insert(16)
tree2.insert(16)
tree2.print_tree()
print(tree2.find(3).value)
print(tree2.find(10))
tree2.delete_tree()
tree2.print_tree()Additional Resources
- A deep dive into Stacks and Queues with plenty of diagrams!
- This overview investigates JavaScript implementations of stacks and queues.
- Looking for more comp sci resources? Check out Khan Academy's tutorials on algorithms and the science of the Internet.
